皆さんご存知の通りDeep Learningの学習には大量の学習データが必要です。実際の問題として学習データを数多く集め、適切なラベルを振るのはとても大変です。私たちは以前からData Augmentationにはお世話になってきていていますし、クロマキー合成でデータ生成をしてみたり、Unityを利用してみたりと色々なことを試してきました。(そういえばスタジオを借りたこともありました)
このあたりの研究は活発なようで、最近でもcutoutとかrandom eraseを見かけます。こうした中で汎用的にData Augumentationが可能なmixupはとても興味深く、いくつか実験も行っています。今回はまずは論文のご紹介からはじめます。
1. mixup とは
mixupのarxivにある論文はこれです。
mixup: Beyond Empirical Risk Minimization
https://arxiv.org/abs/1710.09412 [1]
最新論文はこちらです。
https://openreview.net/forum?id=r1Ddp1-Rb [2]
ICLR 2018 Conferenceに採択されたそうです。
手法としてmixupは以下を実施するだけです。

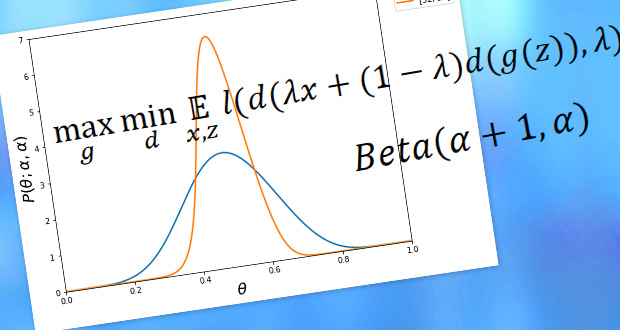
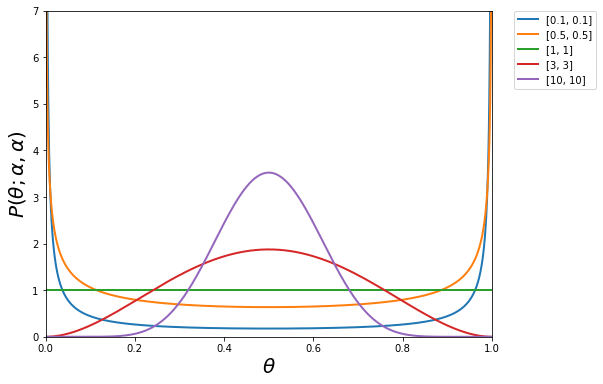
要は2つのデータに対して、ラベル/データ双方を線形補完して新たなデータを作ろうというものです。新たにBeta分布のαがハイパーパラメータとなってしまいますが、ドメイン知識なしでもData Augmentationができるのは興味深いところです。センサーデータなど データを増やす汎用的な方法がなかなか無いもありますので、この手法がうまくいくととてもよいです。なお、Beta分布の確率密度関数は以下の形となります。α=1の場合は一様分布、αが1より小さければ鍋型、1より大きい場合は釣り鐘型になります。
2. mixupの効果
mixupの効果を論文から拾ってみます。参照しているのは最新論文[2]です。
2.1 ImageNet 分類
| Model | Method | Epochs | Top-1 Error | Top-5 Error |
|---|---|---|---|---|
| ResNet-50 | ERM (Goyal et al., 2017) | 90 | 23.5 | – |
| mixup α = 0.2 | 90 | 23.3 | 6.6 | |
| ResNet-101 | ERM (Goyal et al., 2017) | 90 | 22.1 | – |
| mixup α = 0.2 | 90 | 21.5 | 5.6 | |
| ResNeXt-101 32*4d | ERM (Xie et al., 2016) | 100 | 21.2 | – |
| ERM | 90 | 21.2 | 5.6 | |
| mixup α = 0.4 | 90 | 20.7 | 5.3 | |
| ResNeXt-101 64*4d | ERM (Xie et al., 2016) | 100 | 20.4 | 5.3 |
| mixup α = 0.4 | 90 | 19.8 | 4.9 | |
| ResNet-50 | ERM | 200 | 23.6 | 7 |
| mixup α = 0.2 | 200 | 22.1 | 6.1 | |
| ResNet-101 | ERM | 200 | 22 | 6.1 |
| mixup α = 0.2 | 200 | 20.8 | 5.4 | |
| ResNeXt-101 32*4d | ERM | 200 | 21.3 | 5.9 |
| mixup α = 0.4 | 200 | 20.1 | 5 |
表 2-1 [2] Table 1: Validation errors for ERM and mixup on the development set of ImageNet-2012
ImageNet-2012の分類による性能比較。ERMはEmpirical Risk Minimization(経験誤差最小化)の略です。真の分布の期待値からの誤差は期待誤差(expected error)と呼ばれますが、一般には期待誤差を直接評価することができませんので訓練データの誤差(経験誤差/empirical error)で近似します。これを最小化するのがまさしくERMで通常の機械学習の枠組みです。ここでは従来手法のことを指しています。ERMでは標準的なdata augmentationであるスケール、アスペクト比、ランダムクロップ、水平反転など適用しています。mixupについて、αは0.1から0.4の間で実験を行っている。αを大きくしすぎるとunderfittingとなったとのこと。epochs 90 -> 200 でERMは結果がほぼ変りませんがmixupは性能が向上しています。200 epochs でTop1が1%以上違うのはかなりすごい結果ですね。ResNet-50でResNet-101並みの性能が出でているのも注目です。
2.2 CIFAR-10 AND CIFAR-100
| Dataset | Model | ERM | mixup |
|---|---|---|---|
| CIFAR-10 | PreAct ResNet-18 | 5.6 | 4.2 |
| WideResNet-28-10 | 3.8 | 2.7 | |
| DenseNet-BC-190 | 3.7 | 2.7 | |
| CIFAR-100 | PreAct ResNet-18 | 25.6 | 21.1 |
| WideResNet-28-10 | 19.4 | 17.5 | |
| DenseNet-BC-190 | 19 | 16.8 |
表 2-2 [2] Figure 3: Test errors for ERM and mixup on the CIFAR experiments.
CIFAR-10とCIFAR-100での性能比較。Epoch数は200で固定。α=1。これもかなり性能向上しています。αが大きいのはネットワークのパラメータに対してデータ数が少ないからでしょうか。
2.3 SPEECH DATA
Google commands dataset。65,000の発話(utterance)1秒の長さで30クラス。yes, no, down, leftなどの命令を異なる数千人で発話されたものです。16 kHzまでの音を周波数変換した画像(160 x 101)に変換。画像変換後にmixupしました。
mixupのときは最初の5エポックはmixupオフで学習し、その後オンで学習した
そうすると初期の収束が早いことを発見したそうです。
| Model | Method | Validation set | Test set |
|---|---|---|---|
| LeNet | ERM | 9.8 | 10.3 |
| mixup (α = 0.1) | 10.1 | 10.8 | |
| mixup (α = 0.2) | 10.2 | 11.3 | |
| VGG-11 | ERM | 5 | 4.6 |
| mixup (α = 0.1) | 4 | 3.8 | |
| mixup (α = 0.2) | 3.9 | 3.4 |
表 2-3 [2] Figure 4: Classification errors of ERM and mixup on the Google commands dataset
LeNetよりも表現力の高いVGG-11の方で性能向上が見られました。
2.4 MEMORIZATION OF CORRUPTED LABELSMEMORIZATION OF CORRUPTED LABELS
CIFAR-10で20,50,80%の確率でラベルをランダムに変更する(Corrupt)、という実験を行っています。
| Label corruption | Method | Test error | Training error | ||
|---|---|---|---|---|---|
| Best | last | Real | Corrupted | ||
| 20% | ERM | 12.7 | 16.6 | 0.05 | 0.28 |
| ERM + dropout (p = 0.7) | 8.8 | 10.4 | 5.26 | 83.55 | |
| mixup (α = 8) | 5.9 | 6.4 | 2.27 | 86.32 | |
| mixup + dropout (α = 4, p = 0.1) | 6.2 | 6.2 | 1.92 | 85.02 | |
| 50% | ERM | 18.8 | 44.6 | 0.26 | 0.64 |
| ERM + dropout (p = 0.8) | 14.1 | 15.5 | 12.71 | 86.98 | |
| mixup (α = 32) | 11.3 | 12.7 | 5.84 | 85.71 | |
| mixup + dropout (α = 8, p = 0.3) | 10.9 | 10.9 | 7.56 | 87.9 | |
| 80% | ERM | 36.5 | 73.9 | 0.62 | 0.83 |
| ERM + dropout (p = 0.8) | 30.9 | 35.1 | 29.84 | 86.37 | |
| mixup (α = 32) | 25.3 | 30.9 | 18.92 | 85.44 | |
| mixup + dropout (α = 8, p = 0.3) | 24 | 24.8 | 19.7 | 87.67 | |
表 2-4 [2] Table 2: Results on the corrupted label experiments for the best models.
ERMはトレーニングエラーが小さくテストエラーが大きいので過学習しているといえるでしょう。Corruptedはランダムにラベルを変更しているにも関わらずトレーニングエラーが小さくなっています。これはネットワーク中にトレーニングデータを記憶している(MEMORIZATION)と解釈できます。mixupはαを1,2,8,32と変更して実験を行っています。一番いい結果はmixupとdropoutを組み合わせでした。
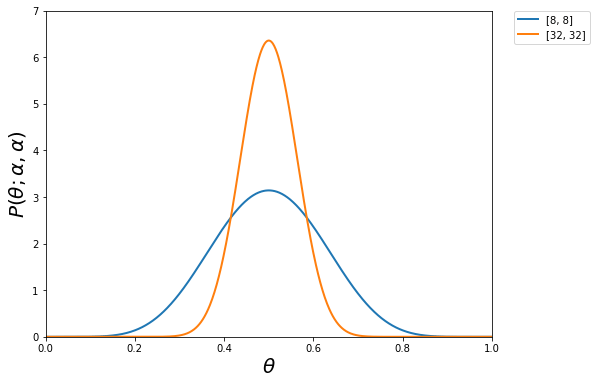
なお、α=8,32のときの確率密度関数はこんな形状です。
2.5 ROBUSTNESS TO ADVERSARIAL EXAMPLES
| Metric | Method | FGSM | I-FGSM |
|---|---|---|---|
| Top-1 | ERM | 90.7 | 99.9 |
| mixup | 75.2 | 99.6 | |
| Top-5 | ERM | 63.1 | 93.4 |
| mixup | 49.1 | 95.8 |
(a) White box attacks.
| Metric | Method | FGSM | I-FGSM |
|---|---|---|---|
| Top-1 | ERM | 57.0 | 57.3 |
| mixup | 46.0 | 40.9 | |
| Top-5 | ERM | 24.8 | 18.1 |
| mixup | 17.4 | 11.8 |
(b) Black box attacks.
表 2-5 [2] Table 3: Classification errors of ERM and mixup models when tested on adversarial examples.
Adversarial examples とは視覚的に知覚できないような小さな摂動を加えることでモデルの性能低下を引き起こすサンプルです。Adversarial examplesに対する堅牢性を改善することは、活発な研究のテーマとなっています。この問題の対応方法はいくつか提案はされていますが、計算上のオーバーヘッドを招きがちです。mixupはオーバーヘッドを回避しつつ堅牢性の向上に役に立ちます。
評価はホワイトボックスとブラックボックスの2種類。ホワイトボックスは2つのモデルのそれぞれについて、高速勾配符号法(Fast Gradient Sign Method /FGSM)及び反復FGSM法(Iterative FGSM /I-FGSM)を使用して、モデル自体を使用して敵対的な例を生成しています。すべてのピクセルについて最大摂動= 4となる。I-FGSMでは、ステップサイズが等しい10回の反復を使用しました。
ブラックボックスについては、最初のERMモデルを使用して、FGSMとI-FGSMを使用して敵対的な例を生成する。次に、第2のERMモデルとmixupプモデルの堅牢性をこれらの例に対してテストしました。
mixupを使うとrobust性は向上が認められます。但しだまされなくなる訳ではないようです。
2.6 TABULAR DATA
| Dataset | ERM | mixup |
|---|---|---|
| Abalone | 74.0 | 73.6 |
| Arcene | 57.6 | 48 |
| Arrhythmia | 56.6 | 46.3 |
| Dataset | ERM | mixup |
|---|---|---|
| Htru2 | 2.0 | 2.0 |
| Iris | 21.3 | 17.3 |
| Phishing | 16.3 | 15.2 |
表 2-6 [2] Table 4: ERM and mixup classification errors on the UCI datasets.
非画像データに対するmixupの性能をさらに調べるために、UCIデータセット(https://archive.ics.uci.edu/ml/datasets.html )から抽出された6つの任意の分類問題に関する一連の実験を実施しました。ここでは隠れ層2のFCスタックで活性化関数はReLUです。最適化関数はAdamで、サイズ16のミニバッチの10回以上にわたって学習しました。数値はテストデータにおけるエラーです。6つの評価すべてでERMを下回るものはなく、大半で性能が改善されています。
2.7 STABILIZATION OF GENERATIVE ADVERSARIAL NETWORKS (GANS)
生成系として盛り上がっているGAN(Generative Adversarial Networks)についてもmixupは有効でした。数学的にGANは以下を最適化する問題と同一です。

mixupによる最適化の式は以下のとおり
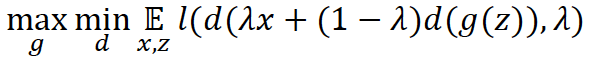
実画像とブレンドするので、discriminatorには難しくなるのではないでしょうか。
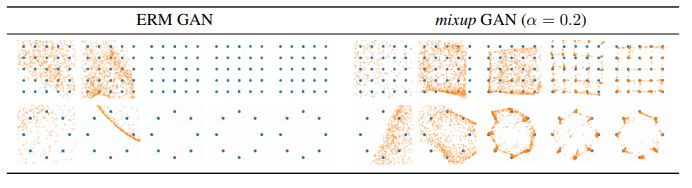
図 2-1 [2] Figure 5: Effect of mixup on stabilizing GAN training at iterations 10, 100, 1000, 10000, and 20000.
mixupの方が安定した生成を実現しているのが見て取れます。
2.8 ABLATION STUDIES
Mixupはラベルとデータを線形補完して新たなラベルとデータを作成していますが、その方法にはいくつか選択肢がありえます。いくつかのバターンで比較実験を行いました。
データセット:CIFAR-10
ネットワーク:PreAct ResNet-18
weight decay は2種類( 10-4, 5 X 10-4 )
| Method | Specification | Modified | Weight decay | ||
|---|---|---|---|---|---|
| Input | Target | 10-4 | 5 X 10-4 | ||
| ERM | X | X | 5.53 | 5.18 | |
| mixup | AC + RP | ✓ | ✓ | 4.24 | 4.68 |
| AC + KNN | ✓ | ✓ | 4.98 | 5.26 | |
| mix labels and latent representations (AC + RP) | Layer 1 | ✓ | ✓ | 4.44 | 4.51 |
| Layer 2 | ✓ | ✓ | 4.56 | 4.61 | |
| Layer 3 | ✓ | ✓ | 5.39 | 5.55 | |
| Layer 4 | ✓ | ✓ | 5.95 | 5.43 | |
| Layer 5 | ✓ | ✓ | 5.39 | 5.15 | |
| mix inputs only | SC + KNN(Chawla et al., 2002) | ✓ | X | 5.45 | 5.52 |
| AC + KNN | ✓ | X | 5.43 | 5.48 | |
| SC + RP | ✓ | X | 5.23 | 5.55 | |
| AC + RP | ✓ | X | 5.17 | 5.72 | |
| label smoothing (Szegedy et al.,2016) | ε = 0.05 | X | ✓ | 5.25 | 5.02 |
| ε= 0.1 | X | ✓ | 5.33 | 5.17 | |
| ε= 0.2 | X | ✓ | 5.34 | 5.06 | |
| mix inputs + label smoothing (AC + RP) | ε= 0.05 | ✓ | ✓ | 5.02 | 5.4 |
| ε= 0.1 | ✓ | ✓ | 5.08 | 5.09 | |
| ε= 0.2 | ✓ | ✓ | 4.98 | 5.06 | |
| ε= 0.4 | ✓ | ✓ | 5.25 | 5.39 | |
| add Gaussian noise to inputs | σ = 0.05 | ✓ | X | 5.53 | 5.04 |
| σ = 0.1 | ✓ | X | 6.41 | 5.86 | |
| σ = 0.2 | ✓ | X | 7.16 | 7.24 | |
表 2-7 [2] Table 5
| AC: | すべてのクラスでmixする |
| SC: | 同じクラスでmixする |
| RP: | ランダムに選んだペアでmixする |
| KNN: | (k=200)のk-近傍のペアでmixする(特徴量が何かは記載なし) |
| label smoothing: | ε/10の確率で誤ったラベルに付け替える |
結果の数値は最後の10エポックのテスト誤差の中央値です。CNN feartureをmixしたりlabel smoothing したりいろいろと評価したが結果としてmixupが一番よいとの結果でした。
2.9 その他の可能性
論文の「5 Discussion」にて、mixupの探索の方向性も議論されています。1つは回帰問題、構造化予測問題への応用、もう一つは教師なし、半教師あり、および強化学習への応用です。mixupはドメイン知識なしにデータ拡張が可能で、かつその計算上のオーバーヘッドがほとんどない点を考えると、色々応用してみたい手法であります。
3. mixupで半教師あり学習?
以下の記事でmixupを再定式化が検討されています。
http://www.inference.vc/mixup-data-dependent-data-augmentation/
これによるとバイナリまたは多項式クロスエントロピー損失を使用する限りにおいて、ラベルのミックスを含まない形での再定式化が可能だった。但しλの分布は以下に変わります。
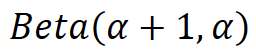
ラベルのミックスなしでデータだけのミックスで対応できるならば半教師あり学習に応用できるはず。是非試してみたいところです。
4. 今後
私たちmixupについてのリサーチと実験を行ってきています。それらのいくつかは別の記事にて報告していきます。