JijZeptによる数理最適化～QUBOを例に～その1：JijZeptとは

JijZeptによる数理最適化～QUBOを例に～その1：JijZeptとは

Posted by Takuma Mitamura 2025/12/16

はじめに

本記事は全3回のシリーズ記事の第1回 です。

その1：JijZeptとは
その2：OpenJijとJijZeptSolver
その3：JijZept Solver の性能検証

「現在地から最も移動距離を少なくして目的地にたどり着きたい」「従業員の希望とお店側の都合を突き合わせてシフト表を作成したい」といった課題に対して、皆さんならどう取り組むでしょうか？
このような課題に対する一つのアプローチとして数理最適化という方法論があります。これは、満たしてほしい条件や制約および問題の答えの「良さ」の基準となるものを数式で表し、それらを満たすような解を求める数学的な枠組みのことを指します。

数理最適化を適用する場合、抱えている問題を抽象化して数式に落とし込んで定式化し、定式化された問題の解を求めるソルバーで解を求めて、その解を評価しフィードバックする、といった手順を踏みます。これらの手順をコンピュータ上で実行するための様々なツールが存在していますが、どれも個別に開発されていて統合した環境を整えるのは難しいのが現状です。

本連載では、その点が解決されているPythonの数理最適化パッケージ群「JijZept SDK」とソルバー「JijZept Solver」を紹介し、別記事で扱った QUBO を例にソルバーの性能を比較・検証します。
連載の第1回では、JijZept SDK と JijZept Solver をご紹介します。

JijZeptとは

JijZept は、数理最適化のための統合プラットフォームです。

複数の数理最適化パッケージがまとめられた「JijZept SDK」のほか、最適化を支援する「JijZept Tools」や 最適化問題を解く「JijZept Solver」、そしてそれらをブラウザ上から利用できる「JijZept IDE」が提供されています。[1]
ここでは JijZept SDK と、JijZept Solver について紹介します。

JijZept SDKとは

JijZept SDK は複数の数理最適化の Python パッケージが含まれた開発キットです。
pip だと次のコマンドでインストールできます。本記事では jijzept_sdk==2025.6.29 を対象とします。

`pip install "jijzept_sdk[all]==2025.6.29"`

上記コマンドでインストールする JijZept SDK には以下のパッケージが含まれています。

パッケージ説明
JijModeling問題を代数的に記述しプログラムで扱える形式にするモデラー
OMMX数理最適化問題の共通データ形式とそれらを扱うためのツールキット
各種 OMMX AdapterOMMX形式の問題を個別のソルバーと繋ぐモジュール
MINTO実験管理のためのライブラリ
Qamomile量子回路を用いる最適化のためのツールキット

ここでは JijModeling と OMMX を取り上げます。

JijModelingとは

最適化問題を解くにあたって、何らかの方法で最適化問題をプログラム上で記述する必要があります。
JijModeling は最適化問題を直感的に記述するために設計されたパッケージです。解きたい最適化問題を数式を扱うのと同じ感覚で記述することができる点が特徴的です。
本記事では jijmodeling==1.12.4 を対象とします。

チュートリアル のコードを見てみましょう：

# jijmodeling をインポート
import jijmodeling as jm

# 「パラメータ」を定義
d = jm.Placeholder("d", ndim=1)
N = d.len_at(0, latex="N")

# 「決定変数」を定義
x = jm.BinaryVar("x", shape=(N,))

# 総和をするためのインデックスを準備
n = jm.Element('n', belong_to=(0, N))

# 数理モデルを管理するオブジェクトを生成
problem = jm.Problem('my_first_problem')
# 目的関数を設定
problem += jm.sum(n, d[n] * x[n])
# 制約条件を設定
problem += jm.Constraint("onehot", jm.sum(n, x[n]) == 1)

パラメータ・決定変数・インデックスを数式で使うような文字で定義・宣言し、解きたい最適化問題とその制約条件を宣言した文字を含む数式で与えます。この例では決定変数 x は0か1の値を取る BinaryVar として宣言されています。この他にも整数を表す IntegerVar や 連続値を表す ContinuousVar などがサポートされています。また、目的関数と制約条件は総和を含む式で与えられています。
このように定式化した最適化問題ですが、Jupyter 上で実行している際に problem を表示させると定式化した問題が LaTeX 形式でレンダリングされた結果が表示されます。

# 数理モデルを表示
problem
\begin{array}{cccc}\text{Problem:} & \text{my\_first\_problem} & & \\& & \min \quad \displaystyle \sum_{n = 0}^{N - 1} d_{n} \cdot x_{n} & \\\text{{s.t.}} & & & \\ & \text{onehot} & \displaystyle \sum_{n = 0}^{N - 1} x_{n} = 1 & \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\ \end{array}

このように定式化した問題を逐次表示することで、決定変数や制約条件等が意図したものになっているか確認することができます。また、この数式の LaTeX 表現は problem._repr_latex_() で文字列として得ることもできます。

print(problem._repr_latex_())
# -> $$\begin{array}{cccc}\text{Problem:} & \text{my\_first\_problem} & & \\& & \min \quad \displaystyle \sum_{n = 0}^{N - 1} d_{n} \cdot x_{n} & \\\text{{s.t.}} & & & \\ & \text{onehot} & \displaystyle \sum_{n = 0}^{N - 1} x_{n} = 1 &  \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\\end{array}$$

この記事のように定式化した問題を別のテキスト媒体に記載したいときには便利な機能です。

OMMXとは

OMMX ( Open Mathematical prograMing eXchange; オミキス)は、最適化問題とそのメタデータを表すオープンなデータ形式とそれを操作するための SDK の総称です。
本記事では ommx==1.9.5 を対象とします。

OMMX とはー図　ソフトウェア同士のデータ交換
図1. OMMX のデータ交換の概念図
引用元：https://jij-inc.github.io/ommx/ja/introduction.html

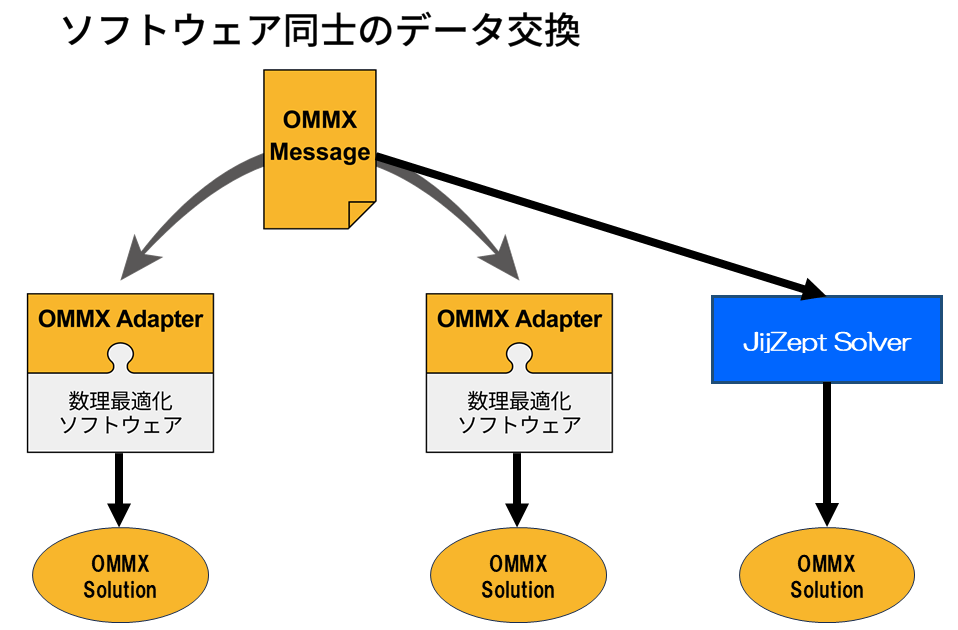
プログラム上では様々なモデリングツールやソルバーを組み合わせて最適化問題を扱うことになりますが、OMMX は共通のデータ形式で最適化問題を表すインターフェースとなるものです。
具体的な値が代入された最適化問題は ommx.v1.Instance クラスのインスタンスで表されます。各ソルバーはふつうommx.v1.Instance型をそのまま入力としては受け付けないので、OMMX Adapter と呼ばれる中間部品を用いて適した入力型に変換して各ソルバーに与えて問題を解くことになります。

例として先ほど JijModeling で定式化した最適化問題 my_first_problem をインスタンス化してみましょう。定式化した数式の中にはパラメータ $d$ が含まれていました。これらに具体的な値を代入することで OMMX インスタンスが得られます。

import ommx

# インスタンスデータ
instance_data = {
    "d": [3, 8, 9, 2, 5] # パラメータ d（1次元配列）に代入する値
}

# OMMX インスタンスを作成
interpreter = jm.Interpreter(instance_data)
ommx_instance: ommx.v1.Instance = interpreter.eval_problem(problem)

JijZept Solverとは

JijZept Solver は JijZept のサービスとして提供されている数理最適化ソルバーです。”OMMX ネイティブ”なソルバーで、先ほど述べた ommx.v1.Instance 型で表された問題を直接引数として与えることができる点に特徴があります。

通常のソルバーでは問題に応じて様々なパラメータを設定して解くことが多いですが、パラメータフリーであり複雑な設定を必要としていない点を売りとしています。また、整数変数や実数変数にも対応しており、幅広い問題クラスに対して一定以上の精度の解を出力することができる能力を持ちます。

JijZept Solverとは 図
図2. OMMX と JijZept Solver の関係（図1を基に作成）

JijZept Solver が利用できる状態として、OMMX インスタンスを入力して問題を解く場合には次のようにします。

import jijzept_solver

# solve メソッドで問題を解く
solution: ommx.v1.Solution = jijzept_solver.solve(ommx_instance, time_limit_sec=2.0)

ソルバーは唯一 solve メソッドが公開されており、OMMX インスタンスと問題を解くのにかけてよい時間 time_limit_sec のみを引数にとります。time_limit_secの上限はソルバーの利用形態によって異なる点に注意が必要です。この引数はソルバーの振る舞いを変えるものではないため、ソルバーとしてはパラメータフリーであることに変わりはありません。一般に、時間をかけるほど精度の良い解が得られる傾向があります。

終わりに

本記事では、Python の数理最適化パッケージ群「JijZept SDK」とソルバー「JijZept Solver」をご紹介しました。
次の記事では、QUBO として表せる基本的な最適化問題を SDK に含まれるソルバーと JijZept Solver で解き、その基本的な性能と傾向を比較します。

[1] 一部サービスは有償での提供です。

Tags: