JijZeptによる数理最適化～QUBOを例に～その2：OpenJijとJijZeptSolver

はじめに

本記事は全3回のシリーズ記事の第2回です。

その1：JijZeptとは
その2：OpenJijとJijZeptSolver
その3：JijZept Solver の性能検証

本記事は、Pythonの数理最適化パッケージ群「JijZept SDK」とソルバー「JijZept Solver」を紹介し性能を比較検証する連載の第2回です。前回は JijZept および周辺のパッケージとソルバーについてご紹介しました。今回は、QUBO として表すことができる基本的な最適化問題を対象に、QUBO を取り扱うパッケージ「OpenJij」に含まれるソルバーと JijZept Solver で解いて基本的な性能や傾向を比較します。

OpenJij とは

OpenJij はイジング模型や QUBO 形式で表された最適化問題のための Python パッケージです。
いくつかのソルバーが同梱されており、その一部は JijZept SDK に含まれる OMMX Adapter「ommx-openjij-adapter」を介して利用することができます。
今回利用するソルバーは、 OpenJij の中で最も標準的な openjij.SASampler（以下、SASampler）と、やや特殊な openjij.SQASampler（以下、SQASampler）です。OpenJij の文脈ではソルバーのことを Sampler と呼んでおり、SA はシミュレーテッド・アニーリング（Simulated Anealing）、SQA は疑似量子アニーリング（Simulated Quantum Anealing）に基づいたソルバーであることを意味しています。
※ QUBO やシミュレーテッド・アニーリング、疑似量子アニーリングに関しての詳しい説明は本記事では割愛いたします。ご了承ください。

ommx-openjij-adapter を介した SASampler で問題を解くには次のようにします。

import ommx
import ommx_openjij_adapter as oj_ad

# openjij.SASampler を利用した Adapter で OMMX 形式の問題を解く
solution: ommx.v1.Solution = oj_ad.OMMXOpenJijSAAdapter.solve(
    ommx_instance, **kwargs
)

SASampler はいくつかのパラメータを持ち、Adaper の solve メソッドを呼び出す際に与えることができます（ここでは kwargs とまとめています）。通常、SASampler で QUBO 形式の問題を解く際は整数引数 num_reads に対応した数の解を”サンプリング”しますが、Adapter の solve メソッドを仲介するとサンプリングした中で最も良い解を一つ自動的に出力してくれます。
記事執筆時点で SQASampler の OMMX アダプターはパッケージとして用意されていません。アダプターを自作するOMMX のチュートリアルも紹介されておりますので、これに従って SQASampler 用のアダプター OMMXOpenJijSQAAdapter を自作しました。

アダプターの定義

from __future__ import annotations

from ommx.v1 import Instance, State, Samples, SampleSet
from ommx.adapter import SamplerAdapter
import openjij as oj
from typing import Optional
import copy

class OMMXOpenJijSQAAdapter(SamplerAdapter):
    """
    openjij.SQASampler 用の自作 OMMX アダプター。
    大部分が openjij.SASampler の実装に基づく。
    """
ommx_instance: Instance

    beta: float | None = None
    gamma: float | None = None
    num_sweeps: int | None = None
    num_reads: int | None = None
    schedule: list | None = None
    initial_state: list | dict | None = None
    updater: str | None = None
    sparse: bool | None = None
    reinitialize_state: bool | None = None
    trotter: int | None = None
    seed: int | None = None

    uniform_penalty_weight: Optional[float] = None
    penalty_weights: dict[int, float] = {}
    inequality_integer_slack_max_range: int = 32

    @classmethod
    def sample(
        cls,
        ommx_instance: Instance,
        *,
        beta: float | None = None,
        gamma: float | None = None,
        num_sweeps: int | None = None,
        num_reads: int | None = None,
        schedule: list | None = None,
        initial_state: list | dict | None = None,
        updater: str | None = None,
        sparse: bool | None = None,
        reinitialize_state: bool | None = None,
        trotter: int | None = None,
        seed: int | None = None,
        uniform_penalty_weight: Optional[float] = None,
        penalty_weights: dict[int, float] = {},
        inequality_integer_slack_max_range: int = 32,
    )  -> SampleSet:
        sampler = cls(
            ommx_instance,
            beta=beta,
            gamma=gamma,
            num_sweeps=num_sweeps,
            num_reads=num_reads,
            schedule=schedule,
            initial_state=initial_state,
            updater=updater,
            sparse=sparse,
            reinitialize_state=reinitialize_state,
            trotter=trotter,
            seed=seed,
            uniform_penalty_weight=uniform_penalty_weight,
            penalty_weights=penalty_weights,
            inequality_integer_slack_max_range=inequality_integer_slack_max_range,
        )
        response = sampler._sample()
        return sampler.decode_to_sampleset(response)

    def __init__(
        self,
        ommx_instance: Instance,
        *,
        beta: float | None = None,
        gamma: float | None = None,
        num_sweeps: int | None = None,
        num_reads: int | None = None,
        schedule: list | None = None,
        initial_state: list | dict | None = None,
        updater: str | None = None,
        sparse: bool | None = None,
        reinitialize_state: bool | None = None,
        trotter: int | None = None,
        seed: int | None = None,
        uniform_penalty_weight: Optional[float] = None,
        penalty_weights: dict[int, float] = {},
        inequality_integer_slack_max_range: int = 32,
    ):
        self.ommx_instance = copy.deepcopy(ommx_instance)
        self.beta = beta
        self.gamma = gamma
        self.num_sweeps = num_sweeps
        self.num_reads = num_reads
        self.schedule = schedule
        self.initial_state = initial_state
        self.updater = updater
        self.sparse = sparse
        self.reinitialize_state = reinitialize_state
        self.trotter = trotter
        self.seed = seed
        self.uniform_penalty_weight = uniform_penalty_weight
        self.penalty_weights = penalty_weights
        self.inequality_integer_slack_max_range = inequality_integer_slack_max_range

    def decode_to_sampleset(self, data: oj.Response) -> SampleSet:
        samples = decode_to_samples(data)
        return self.ommx_instance.evaluate_samples(samples)

    def decode_to_samples(self, data: oj.Response) -> Samples:
        return decode_to_samples(data)

    @property
    def sampler_input(self) -> dict[tuple[int, int], float]:
        qubo, _offset = self.ommx_instance.to_qubo(
            uniform_penalty_weight=self.uniform_penalty_weight,
            penalty_weights=self.penalty_weights,
            inequality_integer_slack_max_range=self.inequality_integer_slack_max_range,
        )
        return qubo

    def _sample(self) -> oj.Response:
        sampler = oj.SQASampler()
        qubo = self.sampler_input
        return sampler.sample_qubo(
            qubo,  # type: ignore
            beta=self.beta,
            gamma=self.gamma,
            num_sweeps=self.num_sweeps,
            num_reads=self.num_reads,
            schedule=self.schedule,
            initial_state=self.initial_state,
            updater=self.updater,
            sparse=self.sparse,
            reinitialize_state=self.reinitialize_state,
            trotter=self.trotter,
            seed=self.seed,
        )

def decode_to_samples(response: oj.Response) -> Samples:
    sample_id = 0
    entries = []

    num_reads = len(response.record.num_occurrences)
    for i in range(num_reads):
        sample = response.record.sample[i]
        state = State(entries=zip(response.variables, sample))  # type: ignore
        ids = []
        for _ in range(response.record.num_occurrences[i]):
            ids.append(sample_id)
            sample_id += 1
        entries.append(Samples.SamplesEntry(state=state, ids=ids))
    return Samples(entries=entries)

このアダプターを介することで、最適化問題を OMMX 形式で表せばOpenJij のソルバー（Sampler）と JijZept Solver の両方で解くことができるようになります。

実験：各ソルバーの基本性能比較

今回は先述の OpenJij のソルバー2種と、第1回記事でご紹介した JijZept Solver の基本的な性能を比較します。

対象問題

以下の基本的な組合せ最適化問題を対象とします。

2次元平面上の点のクラスタリング
ナップザック問題
巡回セールスマン問題（Touring Salesman Problem, TSP）

これらの最適化問題をランダムに生成し OMMX 形式とした上で、jijzept_solver および SASampler・SQASampler（のアダプター）に与えて解を比較します。

実験条件

SASampler, SQASampler は引数として num_sweepsを与えることができます。これは Sampler 内の処理時間に影響するもので、一般に大きいほど実行時間がかかりますが解の精度が良くなる傾向があります。一方 JijZept Solver は time_limit_sec を引数で与えることができ、名前通り実行時間の上限を定めるものです [1]。
num_sweeps および time_limit_sec を変えながら、同じ問題を3つのソルバーで解いて (1)処理時間と (2)目的関数の値を比較します。
ここでは乱数のシードを固定し、後述の各問題サイズ1つあたりに対し1つの問題を評価します。

引数	値のリスト
num_sweeps (for SASampler, SQASampler )	[50, 100, 200, 500, 1000]
time_limit_sec (for JijZept Solver)	[1, 5, 10, 30, 60]

実行環境

本記事における検証の実行環境について記載します。

計算環境

Jij 関連パッケージ・サービスをすべて利用できる Web 上の統合開発環境「JijZept IDE」上に立ち上げた JupyterLab 環境を利用します（2025年7月時点）。

JupyterLab 環境を立ち上げる際のパラメータはデフォルト値のものを採用しています。

Intel® Xeon® CPU @ 2.80GHz が8コア搭載された Ubuntu 22.04 環境で、RAM は 31GB です。GPUは使用しておりません。

主要なライブラリとバージョン

本記事で用いる主なライブラリとそのバージョンを記載します。

ライブラリ	バージョン
jijmodeling	1.12.4
jijzept_sdk	2025.6.29
jijzept-solver	1.0.0
jijzept_solver_ide	2.9.0
ommx	1.9.5
ommx-openjij-adapter	1.9.5
openjij	0.9.2

実験結果

各最適化問題に関して評価結果を記載します。

クラスタリング

参考：アニーリングを用いたクラスタリング

点の数Nを N=50, 100, 200, 500, 1000$ として2つのクラスターを区別できるような2次元平面上の点をランダムに生成し、ラベル付けした点どうしが離れるほど値が小さくなる目的関数を用いて問題を定式化しました。

import jijmodeling as jm

d = jm.Placeholder("d", ndim=2)
N = d.len_at(0, latex="N")
x = jm.BinaryVar("x", shape=(N,))
i = jm.Element("i", belong_to=(0, N))
j = jm.Element("j", belong_to=(0, N))
sigma_i = 2 * x[i] - 1
sigma_j = 2 * x[j] - 1

problem = jm.Problem("Clustering")
problem += -jm.sum([i, j], d[i, j] * (1 - sigma_i * sigma_j))

$\begin{array}{cccc} \text{Problem:} & \text{Clustering} & & \\ & & \min \quad \displaystyle - \sum_{i = 0}^{N - 1} \sum_{j = 0}^{N - 1} d_{i, j} \cdot \left(- \left(2 \cdot x_{i} - 1\right) \cdot \left(2 \cdot x_{j} - 1\right) + 1\right) & \\ \text{{where}} & & & \\ & x & 1\text{-dim binary variable}\\ \end{array}$

この問題においては QUBO に変形する前から制約条件が課されていないため、すべての決定変数の値の組み合わせが実行可能解となります。
評価結果を図1・2に示します。

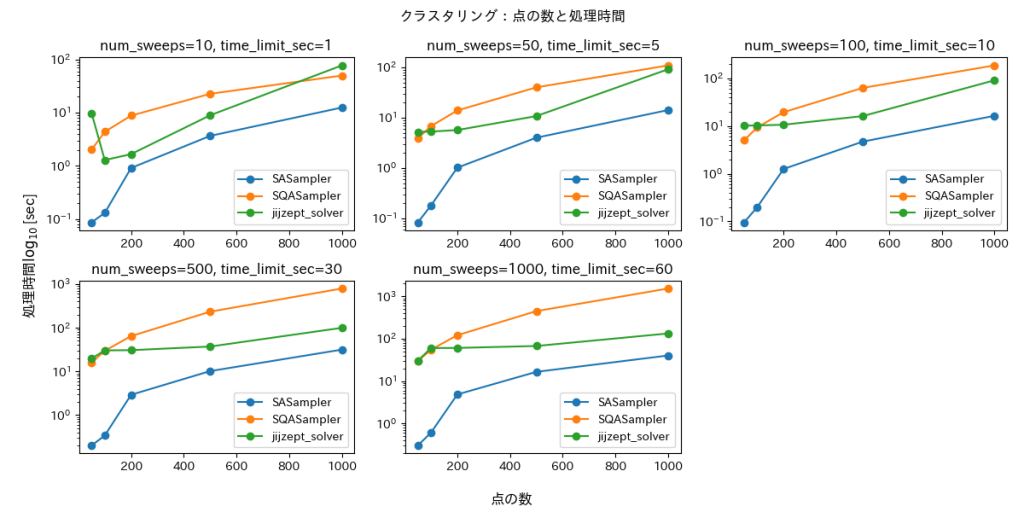
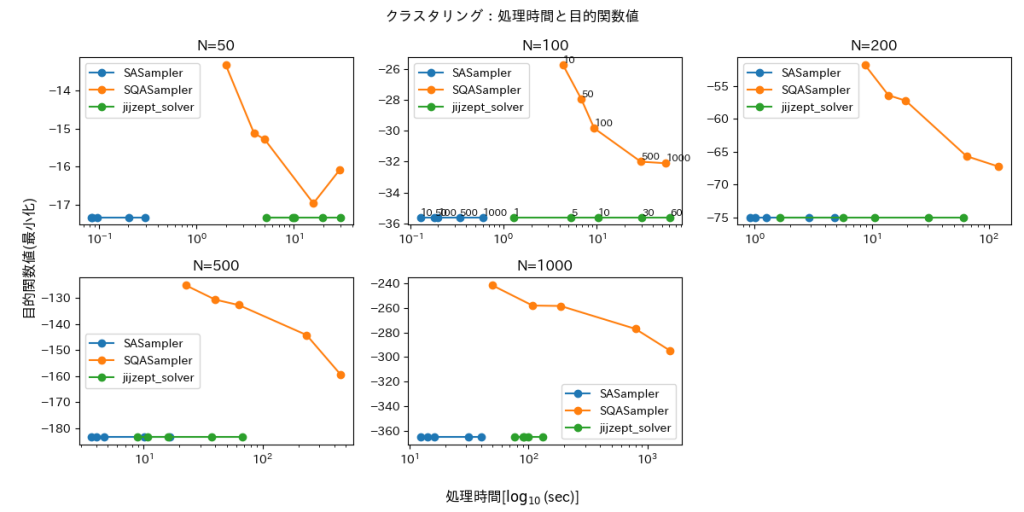
図1の処理時間（対数スケール）を見ると、SASampler・SQASampler は点の数が増えるにしたがって増加していることが見て取れます。time_limit_sec を設定している JijZept Solver に関しては設定した値から大きく変動することはない期待がありましたが、time_limit_sec が小さく問題サイズが大きいほど実際の処理時間が変動しています。これは、問題サイズの増加に伴って通信や実際に問題を解く前後の処理時間が増大しているためでした。

図2は目的関数値の推移です。同じサイズの図中における推移は、ソルバの各パラメータ値（num_sweeps, time_limit_sec）での値を表しています。図から明らかなように、SQASampler は他の2つに比べて実行時間がかかっているにもかかわらず、目的関数値が大きいままとなっています。一方残り2つは目的関数値がほぼ同じスケールとなっており、最適な値に概ねたどり着けている様がうかがえます。

ナップザック問題

参考：ナップサック問題

荷物の数Nを最大容量として、N = 20, 30, 50, 75, 100個の荷物をランダムに生成します。荷物の重さは5～30、価値は（重さ-2）～（重さ+20）とし、重さの合計が最大容量を超えない制約の下で価値の総量を最大化します。制約条件が不等式制約であり、QUBO に変換する際にスラック変数が数個導入されるため、厳密には SASampler・SQASampler と JijZept Solver で全く同じ問題を解いているわけではない点に注意してください。

import jijmodeling as jm

v = jm.Placeholder("v", ndim=1)
w = jm.Placeholder("w", ndim=1)
W = jm.Placeholder("W")
N = v.len_at(0, latex="N")
x = jm.BinaryVar("x", shape=(N,))
i = jm.Element("i", (0, N))

problem = jm.Problem("Knapsack", sense=jm.ProblemSense.MAXIMIZE)
problem += jm.sum(i, v[i] * x[i])

# 制約条件：荷物の総量に関する不等式制約
problem += jm.Constraint("capacity", jm.sum(i, w[i] * x[i]) <= W)

$\begin{array}{cccc} \text{Problem:} & \text{Knapsack} & & \\ & & \max \quad \displaystyle \sum_{i = 0}^{N - 1} v_{i} \cdot x_{i} & \\ \text{{s.t.}} & & & \\ & \text{capacity} & \displaystyle \sum_{i = 0}^{N - 1} w_{i} \cdot x_{i} \leq W & \\ \text{{where}} & & & \\ & x & 1\text{-dim binary variable}\\ \end{array}$

評価結果を図3・4に示します。SASampler・SQASampler に関しては実行可能解を返さないことがあり、10回のリトライの中で解が得られたもののみ結果を描画しています。

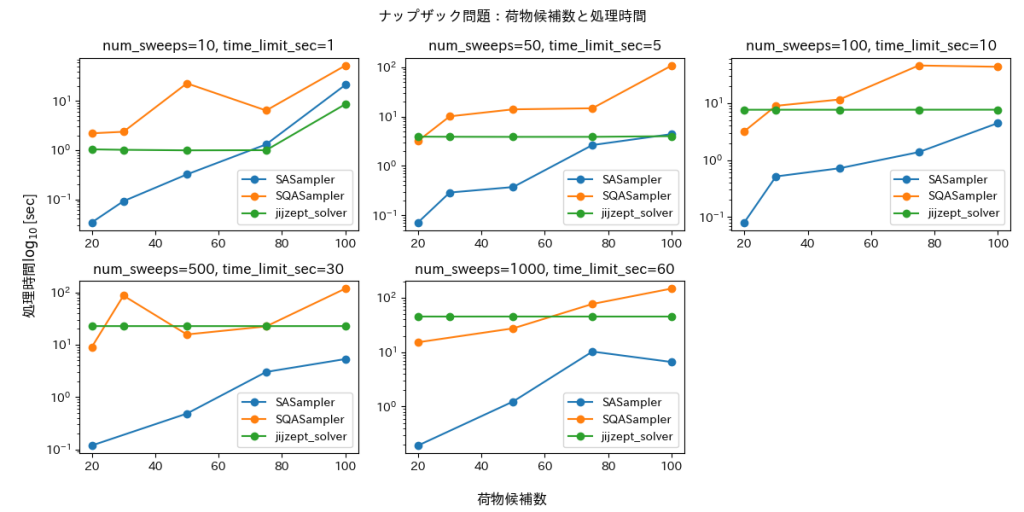
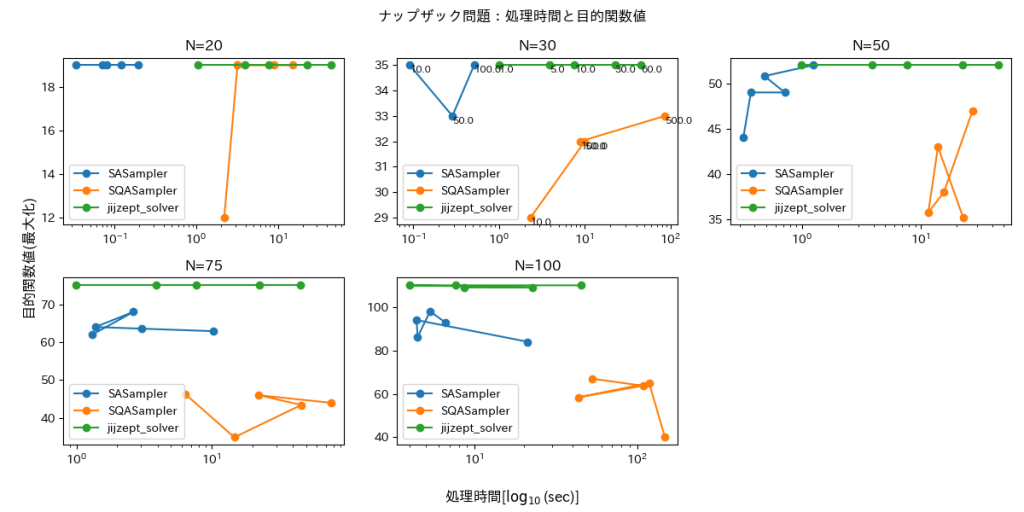
いずれもクラスタリングと同様の傾向にあります。一方で目的関数値を見ると、N=20以外では SASampler は JijZept Solver に比べて目的関数値が低く、荷物の数が多くなるほど安定していないことがわかります。JijZept Solver はどの time_limit_sec においても安定して目的関数を最大化できています。

巡回セールスマン問題

参考：JijModeling+OMMX Adapterを用いた数理モデルの構築とOpenJijでの最適化計算

最後に巡回セールスマン問題(Touring Salesman Problem, TSP)を扱います。都市数 N を N=10, 20, 30, 40, 50 として$[0, 1]\times[0,1]$内にランダムに生成し、標準的な定式化の下で目的関数の最小化を目指します。

import jijmodeling as jm

dist = jm.Placeholder("dist", ndim=2)
N = dist.len_at(0, latex="N")
x = jm.BinaryVar("x", shape=(N, N))
i = jm.Element("i", belong_to=(0, N))
j = jm.Element("j", belong_to=(0, N))
t = jm.Element("t", belong_to=(0, N))

problem = jm.Problem("TSP")
problem += jm.sum([t, i, j], dist[i, j] * x[t, i] * x[(t + 1) % N, j])

# 制約条件1 : 位置に関するonehot制約
problem += jm.Constraint(
    "onehot_location",
    x[:, i].sum() == 1,
    forall=i,
)

# 制約条件2 : 時間に関するonehot制約
problem += jm.Constraint(
    "onehot_time",
    x[t, :].sum() == 1,
    forall=t,
)

$\begin{array}{cccc}\text{Problem:} & \text{TSP} & & \\ & & \min \quad \displaystyle \sum_{t = 0}^{N - 1} \sum_{i = 0}^{N - 1} \sum_{j = 0}^{N - 1} dist_{i, j} \cdot x_{t, i} \cdot x_{\left(t + 1\right) \bmod N, j} & \\ \text{{s.t.}} & & & \\ & \text{onehot\_location} & \displaystyle \sum_{\ast_{0} = 0}^{N - 1} x_{\ast_{0}, i} = 1 & \forall i \in \left\{0,\ldots,N - 1\right\} \\ & \text{onehot\_time} & \displaystyle \sum_{\ast_{1} = 0}^{N - 1} x_{t, \ast_{1}} = 1 & \forall t \in \left\{0,\ldots,N - 1\right\} \\ \text{{where}} & & & \\ & x & 2\text{-dim binary variable}\\ \end{array}$

図5・6に評価結果を示します。

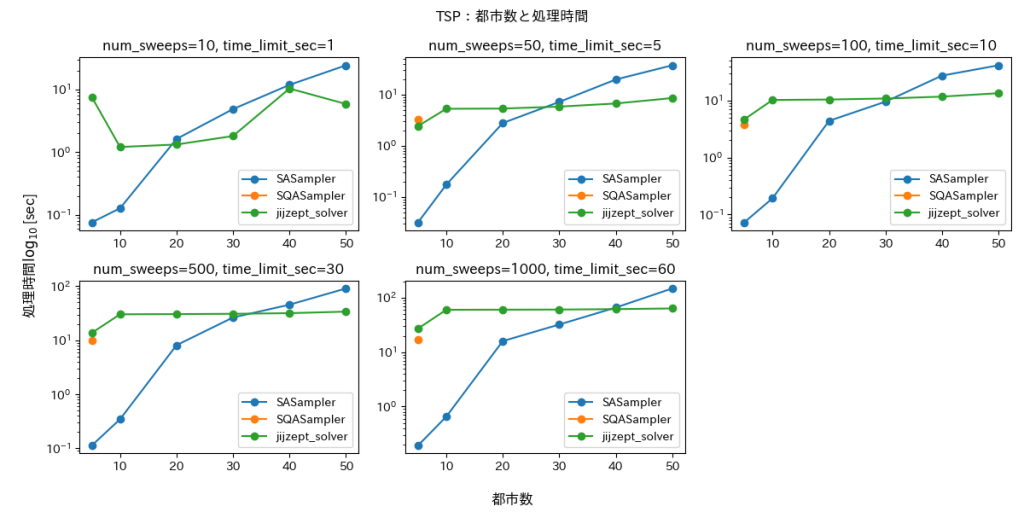
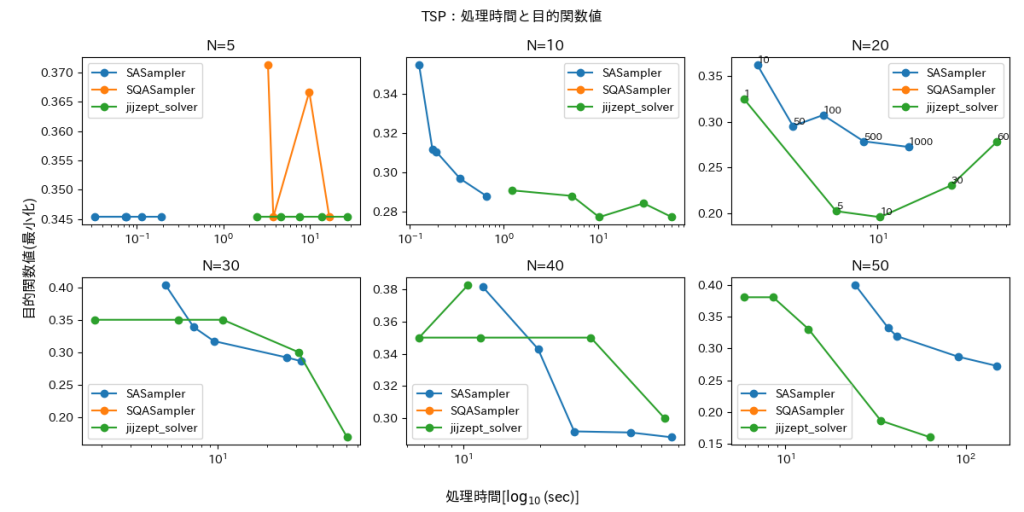
ナップザック問題と同様に、実行可能解が得られたもののみを描画しています。これらの図から SQASampler はほとんどの場合において実行可能解が得られていないことがわかります。SASampler と JijZept Solver は問題によって差がありますが、どちらも一定の解を得ることができています。

終わりに

本記事では、Open Jij に含まれるソルバー2種と JijZept Solver で同じ最適化問題を解いて、性能とその傾向を比較しました。パラメータの違いはありますが、そのうち SASampler と JijZept Solver はある程度安定して良い解を出力することができていました。
次回はこれら2つのソルバーをより詳細に比較します。

[1]: JijZept Solver の利用形態により実行時間の上限値は異なります。

JijZeptによる数理最適化～QUBOを例に～その2：OpenJijとJijZeptSolver

はじめに

OpenJij とは

実験：各ソルバーの基本性能比較

対象問題

実験条件

実行環境

計算環境

主要なライブラリとバージョン

実験結果

クラスタリング

ナップザック問題

巡回セールスマン問題

終わりに

Intel Core UltraのNPUで実現するAIモデル１ CPU附属のNPUを使うには

Pythonスクリプトから実行ファイルを作る方法

PythonとVue.jsで簡単にGUIアプリケーションを作成する方法

Intel Core UltraのNPUで実現するAIモデル2 OpenVINOを使ったNPU推論

Intel Core UltraのNPUで実現するAIモデル3 色々なCNNをNPUで実行する

JijZeptによる数理最適化～QUBOを例に～その1：JijZeptとは

量子アニーリングの古典シミュレーションと数理最適化

Space ROSの「Curiosity rover」デモの実行と拡張(障害物検出と回避)

Intel Core UltraのNPUで実現するAIモデル4 OpenVINOモデルの量子化

WebアプリケーションによるROS2データの可視化4 Webアプリケーション側からのROS2情報送信