概括
$$ \renewcommand{\bra}[1]{\langle #1|} \renewcommand{\ket}[1]{|#1\rangle} \renewcommand{\braket}[2]{{\langle #1|#2\rangle}} $$量子アニーリングとは、量子力学的に状態が重ね合わさった系の基底状態を量子効果を伴いながら探索することで最適化問題の最適解やその近似解を得る技術です [1]。主に組み合わせ最適化問題に用いられるもので、解候補の膨大さから古典的な計算では高速に最適解を得るのが困難な問題に対しても、重ね合わさった状態を効率的に探索し一定の解を出力することができる利点があると考えられています。
2024年に実施した社内勉強会ではこの量子アニーリング技術に着目し、古典手法を用いている既存タスクへの適用可能性を探るほか、具体的な応用を見据えてデモ用アプリケーションを制作し展示会へ出展する等の活動を行いました。
本記事では、量子アニーリングの概要と古典コンピュータ上でのシミュレーションおよび開発したデモ用アプリケーションを紹介します。
量子アニーリングとは
量子アニーリング(Quantum Annealing)は、量子力学の法則を用いてある種の情報処理を行うための枠組みです。特に組み合わせ最適化問題の一般的な解法として位置づけられています。特に、対象となる組み合わせ最適化問題は「イジング模型の最低エネルギー状態(基底状態)を求める問題」です。一般的な組み合わせ最適化問題をイジング模型のハミルトニアンに帰着させ、すべての可能な状態が等確率で重ね合わさった状態から量子力学的な効果を基に基底状態を求めることで最適解ないし近似解を得ます。量子アニーリングは量子ビットを搭載した専用のハードウェア(量子アニーリングマシン、 たとえばD-Wave[2])上で実行されます。
本節では、イジング模型と量子アニーリングの原理を概観し、同様の最適化手法「シミュレーテッド・アニーリング」との差異について紹介します。本節の記述は主に[1]に基づきます。
イジング模型と組み合わせ最適化
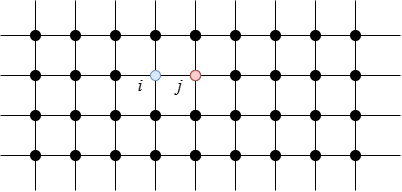
統計力学で用いられる格子模型の一つにイジング模型があります。格子上に並んだ点(格子点)ごとに±1の値を取るイジング変数 \(\sigma_i (i=1,2,…,N)\) が対応付けられており、これらは格子点に配置されたスピンの向き( \(+1\) なら上向き、\(-1\)なら下向き)に対応します。2つのイジング変数 \(\sigma_i,\sigma_j\) の相互作用エネルギーは定数 \(J_{ij}\) を用いて \(-J_{ij} \sigma_i \sigma_j\) と定義されます。
この図ではi, j番目の格子点が隣接している。格子点ごとにイジング変数が対応づけられている。この相互作用エネルギーと、頂点 \(i\) におけるイジング変数・外部磁場 \(h_i\) の積で表されるエネルギー \(-h_i \sigma_i\) のそれぞれの総和を取ったものが系全体のエネルギー
(1)
であり、\(H(\sigma)\) はイジング模型のハミルトニアンと呼ばれます。ハミルトニアンが最小値となるときの \(\sigma=(\sigma_1,\sigma_2,…,\sigma_N )\) を基底状態と呼びます。式(1)には2つのイジング変数の相互作用項のみが含まれていますが、複数のイジング変数の相互作用(多体相互作用)を考えることもできます。
一般に、任意の組み合わせ最適化問題は、多体相互作用を持つイジング模型の基底状態探索問題として定式化できることが知られています。そのため、理論的には多体相互作用を考えればよいわけですが、ハードウェア上の制約などから2体の相互作用のみを考慮することが多いです。さらに式(1)は目的関数のみであり、一般の組み合わせ最適化問題で想定され得る等式・不等式制約は組み込まれていません。そこで、実用上はいくつかの工夫によって3体以上の相互作用の次数を高々2次になるように下げ、等式制約・不等式制約を目的関数に組み込む形に変形します。あわせて、±1の値を取るイジング変数を0,1になるように等価な変換を施すことが多いです。これらの操作によって元の組み合わせ最適化問題は制約条件がなく高々二次のバイナリ変数の項から成る QUBO( Quadratic Unconstrained Binary Optimization )に還元されます。
状態の重ね合わせの行列表現
式(1)はあくまで状態 \(\sigma\)のエネルギーを表しており、状態の重ね合わせの表現にはなっていません。これを量子力学の道具を使って、状態の重ね合わせを表すように書き換えます。特に、理解しやすいかつ計算機上で扱いやすいようにベクトルと行列で表していきます。
まず、1スピンだけから成る模型を考えます。先ほどまで \(\sigma_i=\pm{1}\) と書いていたイジング変数をそれぞれ2次元ベクトル
$$ \begin{pmatrix} 1\\0 \end{pmatrix},\begin{pmatrix} 0\\1 \end{pmatrix} $$に対応させます。実はこの2つのベクトルは、パウリ行列の \(z\) 成分と呼ばれる次の行列
$$ \hat{\sigma}^z:=\begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix} $$の固有値1および-1の固有ベクトル(固有状態)となっていることが言えます。この2つのベクトルの規格化された線形結合
$$ \psi= \frac{1}{\sqrt{|a|^2+|b|^2}}\left(a\begin{pmatrix} 1\\0 \end{pmatrix}+b\begin{pmatrix} 0\\1 \end{pmatrix}\right)=\frac{1}{\sqrt{|a|^2+|b|^2}}\begin{pmatrix} a\\b \end{pmatrix} $$が、スピンが±1の2つの状態が同時に存在する量子力学的重ね合わせを表現していると解釈できます。実際に測定された際に状態が確定しますが、その状態となる確率は各係数の絶対値の2乗が対応しています。
これで状態の重ね合わせが表現できました。基底状態を探索したいので、スピンの±1を適宜入れ替える処理を追加したいところです。これはパウリ行列の \(x\) 成分と呼ばれる行列
で実現できます。実際、これを先ほどの2つのベクトルに作用させると、
$$ \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix}\begin{pmatrix} 1\\0 \end{pmatrix}=\begin{pmatrix} 0\\1 \end{pmatrix}, \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix}\begin{pmatrix} 0\\1 \end{pmatrix}=\begin{pmatrix} 1\\0 \end{pmatrix} $$となります。
以上の道具立てによって、状態の重ね合わせと入れ替えを表現できました。
複数のスピンが存在する場合には、各スピンに対応する2次元ベクトルのテンソル積が状態に対応します。たとえば2つのスピンが存在する場合は \(2\times 2=4\)次元のベクトルで状態が表され、パウリ行列も同様に拡張され \(2^2\times2^2=4\times 4\)の行列となります。
一般に、\(N\)個のスピンがある場合は状態は\(2^N\)次元のベクトルで表され、パウリ行列は \(2^N\times 2^N\)のサイズになることが言えます。
一々ベクトルで書いていると大変なので、ディラックのブラケット記法を用いることが多いです。つまり、
$$ \require{physics} \ket{\uparrow}:=\begin{pmatrix}1\\0 \end{pmatrix}, \ket{\downarrow}:=\begin{pmatrix}0\\1 \end{pmatrix} $$とします。この記号(ケット記号)を使って先ほどの線形結合を \(\psi\) ではなく \(\ket{\psi}\) と書き、これを状態ベクトルと呼びます。括弧を逆向きにした記号はブラ記号と呼ばれ、\(\bra{\psi}=\ket{\psi}^\ast\)(共役転置; 随伴)に対応します。また、2つの状態ベクトル \(\ket{a}, \ket{b}\) の内積は \(\braket{a}{b}\) と表します。2つのスピンがどちらも上向きである状態はそれぞれの状態ベクトル \(\ket{\uparrow}_1,\ket{\uparrow}_2\)のテンソル積であり、\(\ket{\uparrow}_1\otimes\ket{\uparrow}_2=\ket{\uparrow}_1\ket{\uparrow}_2=\ket{\uparrow\uparrow}\) などと書きます。
量子アニーリング
引用元:https://amplify.fixstars.com/ja/techresources/annealing-method/
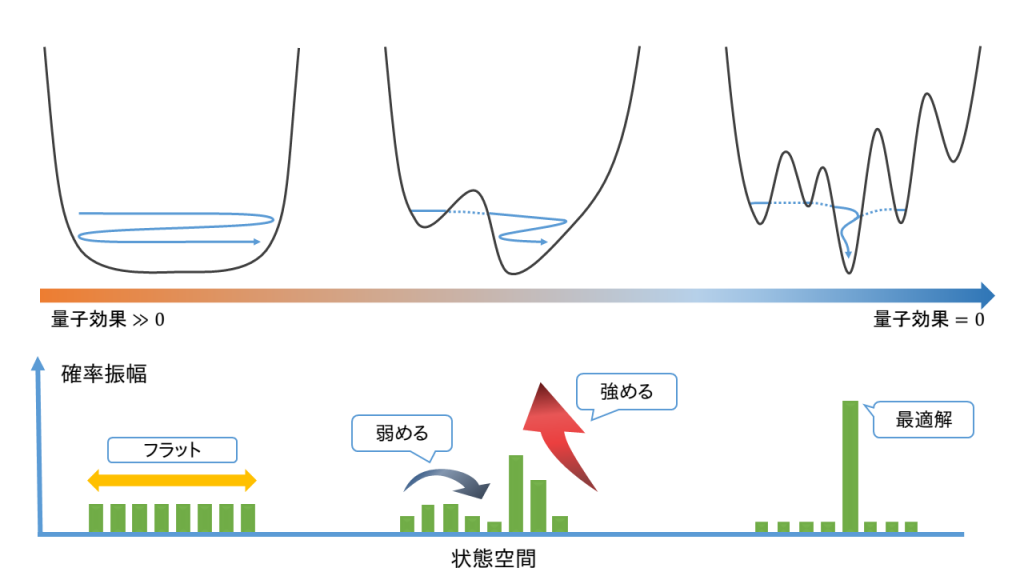
前節で状態とその重ね合わせ・入れ替えを表現できました。すべての状態が等確率に重ね合わさった状態から状態が時間と共に変化していくようにしてイジング模型の基底状態を求めるのが量子アニーリングです。「時間と共に変化していく」ことを表す方式としてここではシュレディンガー方程式を採用します。他の方式や理論的な詳細については[3]を参照してください。
状態の重ね合わせと入れ替えを実現するために、古典イジング模型のハミルトニアン(式(1))中のイジング変数をパウリ行列の \(z\) 成分に書き換え、さらに入れ替えを表すパウリ行列の \(x\) 成分の項を追加します。ただし、最も簡単な例として外部磁場( \(h_i\)の項 )は無いものとしています。
(2)
第1項は元々の組み合わせ最適化問題の目的関数を表しています。一方、スピンの向き(上下=縦)に対して横向きに対応する第2項は横磁場項と呼ばれます。
量子アニーリングにおいては、この \(\Gamma\) が時間依存する(\(\Gamma=\Gamma(t)\))と考え、時刻0において \(\Gamma\) が第1項よりも非常に大きいように取ります。このときハミルトニアンは横磁場項だけから成ります。計算は割愛しますが、横磁場項だけから成るハミルトニアンの基底状態は \(2^N\) 個の状態が等確率に重ね合わさった状態となっています。この状態を出発点として、\(\Gamma\) をゆっくりと減少させていき、系を(時間依存の)シュレディンガー方程式
に従って時間発展させます(ここで \(\hbar\) はプランク定数ですが、簡単のために計算上では1としてしまうことにします)。このとき、\(\Gamma(t)\) の時間変化が”十分ゆっくり”なら、状態 \(\ket{\psi(t)}\) は時刻 \(t\) におけるハミルトニアンに対する定常状態のシュレディンガー方程式
$$ \hat{H}(t)\ket{\Phi_t}=E_0(t)\ket{\Phi_t} $$の基底状態 \(\ket{\Phi_t}\) に十分近いことが知られています。
つまり、大雑把にまとめると次のような工程で量子アニーリングは進みます:
- 対象の組み合わせ最適化問題の目的関数をイジング模型の形で表す
- 1のイジング模型中のイジング変数をパウリ行列に置き換え、横磁場項を加える
- 横磁場項の係数 \(\Gamma\) を時刻0で非常に大きい値にする
- シュレディンガー方程式に従って時間発展させる
- 係数 \(\Gamma\) の時間変化は”十分ゆっくり”にする
- このとき、状態 \(\ket{\psi(t)}\) はその瞬間の定常状態のシュレディンガー方程式の基底状態に十分近い(=基底状態に十分近い状態を辿りながら変化する)
- 十分大きい \(t\)(理想的には \(\infty\) の極限)で \(\Gamma=0\) として、元の目的関数だけから成るハミルトニアンの基底状態に十分近い状態を得る
工程4の「シュレディンガー方程式に従って時間発展させる」ことは特別なアルゴリズムを伴うものではないため、自然に/自律的に最適化問題の解に到達していく、というのが特徴的であると考えられます。”十分ゆっくり” \(\Gamma(t)\) を小さくしていくことが重要で、\(\Gamma(t)\) が一定の条件を満たせば非常に高い確率で目標の基底状態に収束することが知られています[1][3]。
シミュレーテッド・アニーリングとの差異
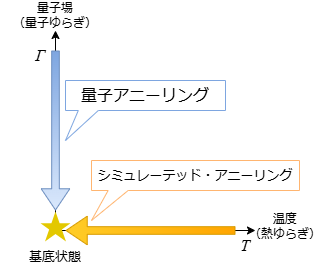
ここまでで量子アニーリングとその原理について見てきました。量子アニーリングはイジング模型のハミルトニアンを横磁場項の効果(量子ゆらぎ)を用いて解を探索するものでした。一方、熱ゆらぎを表す古典的な確率過程で解を探索するのが古典アルゴリズムの一つ「シミュレーテッド・アニーリング[4]」です。
| 量子アニーリング | シミュレーテッド・アニーリング | |
|---|---|---|
| 状態の遷移 | 量子ゆらぎ | 熱ゆらぎ |
| 対応する変数 | 横磁場の係数 \(\Gamma(t)\) | 温度 \(T(t)\) |
| 時間発展 | シュレディンガー方程式など | マスター方程式, マルコフ連鎖モンテカルロ法 |
ここでは詳細は割愛しますが、シミュレーテッド・アニーリングは系のエネルギーが小さいほど確率が高くなるギブス・ボルツマン分布に基づいて解をサンプリングします。このギブス・ボルツマン分布は温度に依存するもので、量子アニーリング同様に”十分ゆっくり”と温度を0に向かって下げながら順次サンプリングしていくことで時刻の極限において非常に高い確率で基底状態に収束することが知られています[1][3]。
両者の動作原理は全く異なりますが、量子アニーリングもシミュレーテッド・アニーリングも、図3のように乱雑/高温の状態から徐々にエネルギーの低い状態に向かって時間発展していく点で類似していると言えます。
最適化手法としての性能差には議論があります。どちらも”十分ゆっくり”横磁場の係数・温度を下げていく必要があり、その減少具合が比較の対象となります。最悪ケースの場合においては量子アニーリングの方が減少具合が大きい=収束が速いですが、最悪ケースでない場合は個別の問題に依存した解析が為されています[1][3]。また、横磁場の係数・温度の減少具合だけでなく、最終的に基底状態の実現確率の大きさも解析対象となっています[3]。
疑似量子アニーリング:量子アニーリングの古典シミュレーション
量子アニーリングは量子アニーリングマシンと呼ばれる専用ハードウェア(量子コンピュータ)上で実行します。その一例としてD-Waveマシン[2]がありますが、コスト面で現状それらに定常的にアクセスし続けるのは難しいと言えます(何より個人所有などできない点が大きいと考えられます)。そこで、量子アニーリングの振る舞いを古典コンピュータ上で疑似的にシミュレーションしようとする試みが為されてきています。この古典シミュレーションを「疑似量子アニーリング」と呼ぶこともあります。
古典シミュレーションには量子モンテカルロ法と呼ばれる手法を用います。これは古典的なシミュレーテッド・アニーリングを援用するもので、量子力学的に再定式化されたハミルトニアンに基づく分配関数を古典的なイジング模型のハミルトニアンで近似→マルコフ連鎖モンテカルロ法を適用するアイデアに基づいています。必ずしも量子アニーリングと同じ振る舞いをするものではないですが、大きく外れた振る舞いをしないだろうという理論的な観点からの期待もあり研究・実装が進められているものです。この利点を突き詰め、疑似量子アニーリングを大規模・高精度に実行する疑似量子アニーリング専用のマシンを開発する大企業も存在します。
古典シミュレーションの応用例
1章「概括」で言及した社内勉強会の活動では、前節で述べた疑似量子アニーリングを取り扱い、具体的な問題を対象としたデモアプリを作成しました。実装は JijModeling および OpenJij によります。
ここではその問題設定と成果物について紹介します。
問題設定と観点
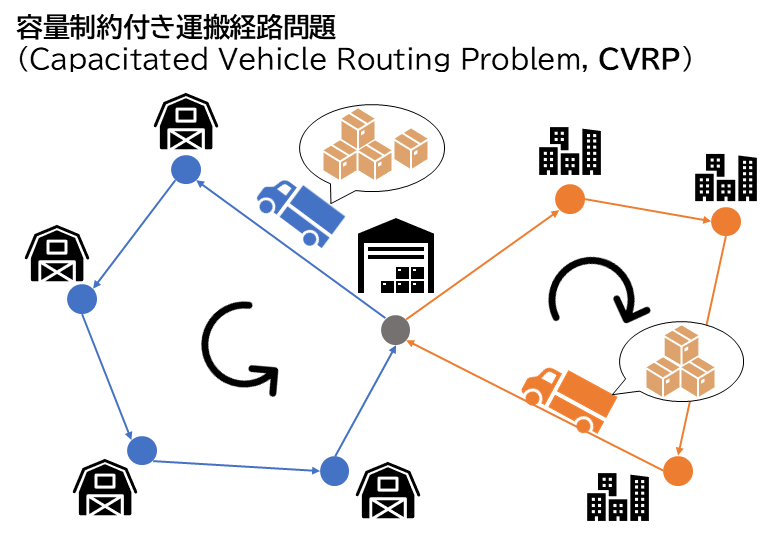
社会問題の解決という具体的な応用も加味して、題材として「物流の最適化」を選びました。つまり、ある物流拠点から各配送先への最適な経路を算出し、各トラックで最適な積み付けを行うことで配送を支援するシステムです。配送計画だけ考えればこれは組み合わせの問題であり、量子アニーリングと非常に相性がよいのも選定理由の一つで、業界にも実例が存在します[5][6]。 「物流の最適化」に対応する問題として、容量制約付き運搬経路問題(Capacitated Vehicle Routing Problem, CVRP)を考えます(図4)。ある配送拠点といくつかの配送先があり、トラックの積載容量が与えられ各配送先には配送拠点から運ぶべき荷物の容量が設定されています。これらの配送先へ最も効率的に荷物を運びきるのが目的であり、これを最適化する対象はトラック数や時間、総移動距離などが考えられますが、ここでは各トラックの移動距離の総和を最小化する問題を考えます。CVRPはトラックへの効率的な荷物の積み付けと効率的な経路の探索を含む点で、ナップザック問題と巡回セールスマン問題(TSP)の混合と解釈することができます。
CVRPを量子アニーリングで解く場合、まず、すべての条件を量子アニーリング向けに落とし込む定式化が考えられます[7]。この定式化の場合、すべてのトラック・配送経路について同時に考えるため探索空間に大域的最適解が存在することが保証されますが、用いる変数が多く問題サイズが大きくなることに伴うデメリット(十分な解を得るまでの時間の増大、解の質の低下)があります。
そこで、先行研究 [8]を参考に問題の分割と古典-量子のハイブリッド手法を考えます。上述の通りCVRPはナップザック問題とTSPの混合問題と見做すことができるため、(1)ナップザック問題を解く段階、(2)TSPを解く段階の2段階に問題を分割します(図5)。(1)は所与のトラック数分のクラスターを構成するように配送先をクラスタリングする処理である。このとき各クラスターには配送拠点を含めることとして、クラスターに含まれる配送先で必要な荷物容量の総和はトラックの積載容量を超えないようにします。この処理によって各トラックが各々のクラスターに含まれる配送先を担当し効率的に回る経路を探索する問題を考えればよいことになります。これが(2)の処理であり、TSPそのものと言えます。問題の分割によって各段階で異なるロジックを適用でき、さらに問題サイズが縮小するほか、(2)のTSPに関しては各クラスターで構成される問題は独立なためクラスター並列で問題を解くことができて、時間短縮にも繋がるという利点があります。
デモアプリではこの方式を全面的に採用し、複数の小さな問題を並列で解くことで解精度の向上と高速化を図りました。
成果物
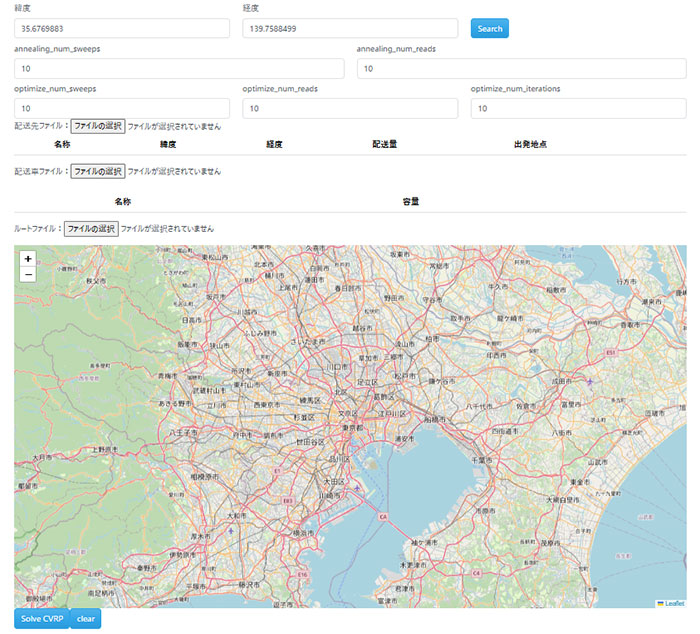
最終的にデモアプリは次のような形になりました。図6にデモアプリの画面を示します。
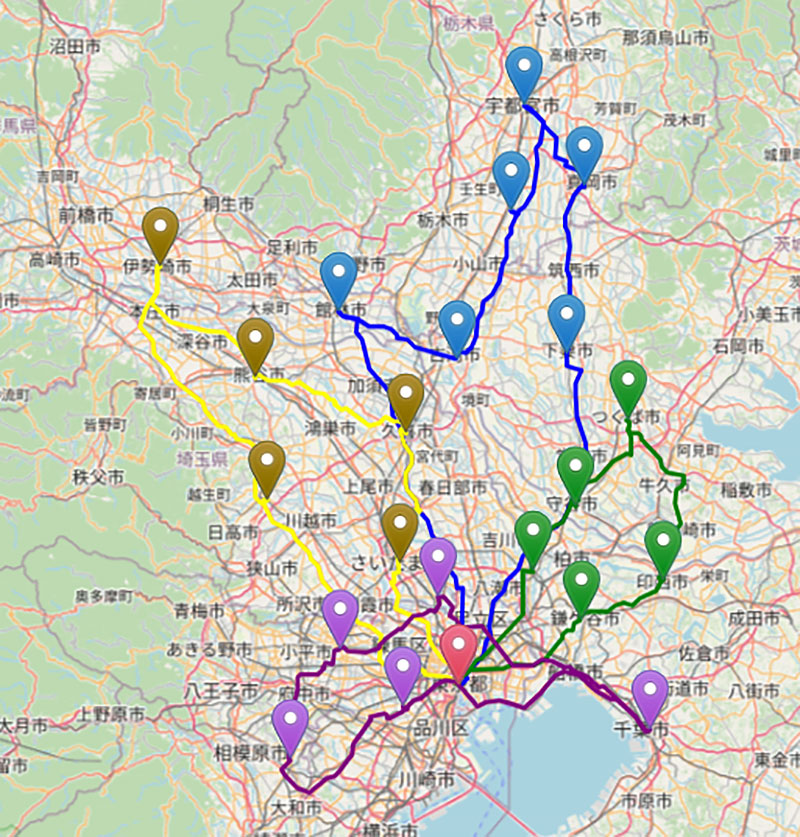
入力として物流拠点・配送先の緯度経度および必要な荷物の量を記載したcsvファイルと、トラックの情報を記載したcsvファイルを与えます。そして疑似量子アニーリングの実行に関する設定を適宜施して最適化を行い、得られた経路を地図上に重畳表示する形です。ここでは各配送先間の経路情報は事前に算出し、ファイルとして出力しています。得られた解(都市と経路)から、この経路情報を基に対応する経路を表示しています。図7はサンプルとして用意した問題(都市数22、トラック数4)の解として出力された経路を表示したものです。
物流拠点を始点・終点としながら、概ね地域ごとに都市をまとめて回るべき経路を決定できていることが分かります。
まとめ
量子アニーリングの原理および古典アルゴリズムの一種「シミュレーテッド・アニーリング」および量子アニーリングの古典シミュレーションについて概観しました。また、古典シミュレーションを活用したデモ用アプリケーションの問題設定と成果物についても報告しました。
また、「成果物」で紹介したデモアプリを携えて2024年5月に開催された「第4回量子コンピューティングEXPO【春】」に出展しました。
第4回【春】はDX推進・最新技術を主眼に置いたNexTech Weekという大規模な展示会の一部として開催されたもので、約30社が出展しました。ISPブースに立ち寄った方の多くは量子技術の情報収集を目的としていましたが、次いで物流関係の企業に所属している方が多かった印象です。「通行止めも考慮したい」「別の経路をすぐに再計算できるか?」「現場のノウハウもシステムに組み込めると嬉しい」などのご質問・ご意見をいただきました。
これはデモアプリの題材を選んだ狙い通りで、DX推進による物流効率化のニーズがあることが確認できた形と言えます。
参考文献
[1] 西森秀稔, 大関真之, “量子アニーリングの基礎,” 共立出版, 2018.
[2] https://www.dwavequantum.com/
[3] S. Tanaka, R. Tamura, B. K. Chakrabarti(共著),田中宗, 田村亮(共訳), “量子アニーリングの物理,” 森北出版, 2023.
[4] S. Kirkpatrick, C. D. Gelatt, Jr. and M. P. Vecchi, “Optimization by Simulated Annealing,” Science, vol. 220, no. 4598, pp. 671-680, 1983.
[5] https://pr.fujitsu.com/jp/news/2024/01/23.html
[6] https://www.magellanic-clouds.com/blocks/solution/logistics-optimization/
[7] https://amplify.fixstars.com/ja/demo/cvrp
[8] S. Feld et al., “A Hybrid Solution Method for the Capacitated Vehicle Routing Problem Using a Quantum Annealer,” Front. ICT, vol. 6, p. 13, Jun. 2019, doi: 10.3389/fict.2019.00013.


![図5. 問題の2段階分割([8, Figure 1])](https://wazalabo.com/wp-content/uploads/2025/12/fict-06-00013-g001.jpg)