問題のモデル化
検出ロジックを考えるにあたり、まずは問題をモデル化します。以下、条件付き確率の基本的な知識があることを想定しています。
画像の情報はRGBの値(画素値)がただ並んでいるだけの配列であり、人がいるかどうかを判断するためには何らかのモデル化(定式化)が必要です。
ある時刻において、
を人物の位置(今回は2次元座標空間),
を観測値(今回は実画像、すなわち画素値の配列)とします。一般に
は状態ベクトル,
は観測データと呼ばれます。
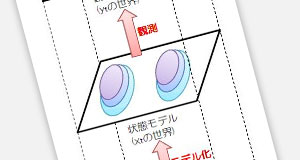
この図のようにモデル化とは現実世界を簡略化・抽象化し、,
の世界(空間)で問題を考える事です。※1このモデル化された世界をそれぞれ状態モデル、観測モデルと呼ぶことにします。以下、これらのモデルについて詳しく述べていきます。
まず状態モデルの空間を、現実世界から、ある確率分布に従って生成されたものと仮定し、これを
・・・(1)
と表します。※2(ここで記号は、左辺の変数が右辺の確率分布に従うことを意味します。)ある座標
における
の値が大きい程、人が位置
に存在する確率が高いことを意味すると考えてください。
また、今回の問題設定では白い背景の前を人が動くことになっているので、人の位置が変わればそれに応じて画素値の配列も変わることが予想されます。つまり観測データは状態ベクトル
に確率的に依存すると考えられ、条件付き確率を用いて
・・・(2)
と表されます。※3
現実世界からではなく、の世界から
の世界(画像)が観測されたと考えるわけです。確率を用いて表現するのは、影やノイズなどの不確定な要素を考慮する必要があるためと考えることもできます。
ここで改めて今回の目的を思い出してみましょう。目的は「単色背景上を動く人物の重心座標を求めること」でした。我々が直接得ることができる情報は、ある時刻における画像
のみです。ここから、人物の位置
を推定する必要があります。
すなわち、「観測ベクトルが与えられた時の状態ベクトル
の条件付き確率分布
を求める」ことが今回の目的です。※4
は、Bayesの定理を用いることで
・・・(3)
と変形できます。すなわち(3)式の右辺を計算することが当面の目標となります。
次回はこの式を計算する方法について述べていきます。
※1 厳密にはそれぞれ確率空間であり、必ずしも2次元平面で図示できるわけではありませんが、ここではイメージを優先しました。
※2 通常、は、一時刻前の位置
に依存すると考えられるため、
に従うと仮定するのが一般的ですが、今回は時刻依存性を仮定していません。
※3 (1),(2)式をまとめて状態空間モデルと呼びます。
※4 より正確にはの期待値を求めることになります。