動体検出　その３

確率分布の近似

前節で、(3)式の計算を行うことが当面の目標と述べました。ここでは、これらの条件付き確率分布を計算機上で表現する方法について述べます。

確率分布は一般に様々な形状をとるため、定式化することは困難です。ガウス分布の線形和などで近似する方法もありますが、分布の次元が大きくなるに従って計算量が増加してしまい、現実問題を解くのに適さない場合が多々あります。そこで計算機上では、確率分布の実現値（サンプル）を用いてその分布自体を表現します。

いま、 $N$ 個の実現値の集合 $X_t \equiv \{ x_t^{(i)} \}_{i=1}^N$ を用いて分布を表すことを考えます。ここで $x_t^{(i)}$ は時刻 $t$ における確率分布 $p(x_t|y_t)$ の $i$ 番目の実現値を表し、以後、これら各々の実現値を粒子（パーティクル）と呼ぶことにします。

これら $N$ 個の粒子を用いると、(3)式の確率分布は次のように近似できます。
$\displaystyle p(x_t|y_t) \simeq \frac{1}{N} \sum_{i=1}^N \delta(x_t-x_t^{(i)})$ 　・・・(4)
ここで $\delta(\cdot)$ はデルタ関数を表し、括弧の中が0の時は1，それ以外の時は0をとる関数です。これを確率分布のモンテカルロ近似と呼びます。

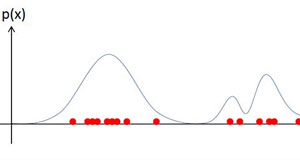
モンテカルロ近似のイメージを以下に示します。

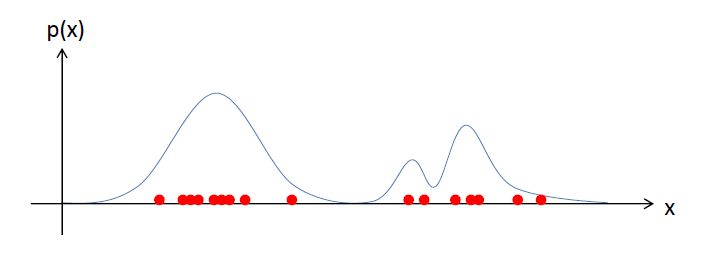
赤い点が各々の粒子を表しています。(4)式の意味がよくわからない場合、赤い点が密なところほど確率分布の山が高く、疎なところほど山が低いと考えて下さい。粒子を用いることで、色々な形の分布が表現できることがわかると思います。このように、求めたい確率分布が（簡単には）定式化できない形をしている場合にモンテカルロ近似は有効な手段となります。

では、確率分布をうまく表現する（すなわちよりよい近似を得るためには）、粒子をどう作ってやればいいでしょうか？粒子を生成することをここではサンプリングと呼びます。例えば一様乱数を用いて粒子をサンプリングしただけでは、求めたい確率分布によく適合するとは限りません（疎密がうまく表現できていません）。

個々の粒子 $x_t^{(i)}$ を生成する確率は、(3)式を用いて
$\displaystyle p( x_t = x_t^{(i)} | y_t ) = \frac{ p(y_t|x_t^{(i)}) p(x_t^{(i)}) }{ \sum_{i=1}^N p(y_t|x_t^{(i)}) p(x_t^{(i)}) }$
と表されますが、分母は確率を1とするための正規化定数なので考慮しないことにすれば、
$\displaystyle p( x_t = x_t^{(i)} | y_t ) \propto p(y_t|x_t^{(i)})p(x_t^{(i)})$ 　・・・(5)
と書けます。

いま $p(x_t^{(i)})$ については全く情報がないので、等確率すなわち $p(x_t^{(i)}) = \frac{1}{N}$ とします。^※1これは、画像全体に粒子を等確率でばらまくことを意味します。また $p(y_t|x_t^{(i)})$ は、粒子 $x_t^{(i)}$ の位置に人がいる画像が得られる確率を表し、これは画像の色情報から計算（具体的には、白壁では確率が低く、それ以外では高くなるように設計）します。これを $N$ 個すべての粒子について計算し、その値に比例するように粒子をサンプリングすれば、求めたい確率分布をうまく表現した近似が得られます。

次回は具体的なサンプリングの方法について述べたいと思います。

※1　（詳しい人向けの注釈）
Bayes推定の用語を用いると、これは無情報事前分布と呼ばれます。無情報事前分布を用いたのは、複数人の検出を行う必要があることも関係しています。
前回と今回（そして次回）の内容は、動体追跡でよく用いられるパーティクルフィルタをもとに、そこへの発展を意識して議論の展開をしています。通常のパーティクルフィルタでは、一時刻前の粒子 $\{x_{t-1}^{(i)}\}_{i=1}^N$ から尤度を計算し、その尤度に比例するように現時刻の粒子 $\{x_t^{(i)}\}_{i=1}^N$ をリサンプリングします。しかし、複数の動体が増減する環境において、パーティクルフィルタは新しい動体をうまく追跡しない（一時刻前の尤度にひきずられてしまう）ことも多く、何らかの工夫が必要となります。
今回は動体のみ行うので、各粒子は一時刻前の情報をすべて忘れて画像の全範囲を探索しにいくことで、動体の増減に対応することにしました。これが数式の上では、無情報事前分布（一様分布）を利用することに相当しています。