動体検出　その４

サンプリング

前節では確率密度関数を有限個の粒子によって近似する方法について説明しました。今回はその粒子を生成（サンプリング）する方法について述べます。

前節の(5)式から、各粒子は確率密度関数に比例するようにサンプリングする必要があります。ここでは簡単のために、ある確率密度関数から個の粒子をサンプリングすることを考えます。計算機上でこれを実現するために、累積分布関数

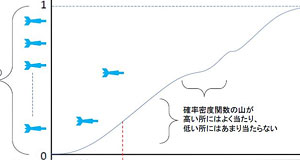
を使ってサンプリングを行う方法がよく用いられます。次の図を見てください。これは、サンプリングアルゴリズムのイメージを表したものです。

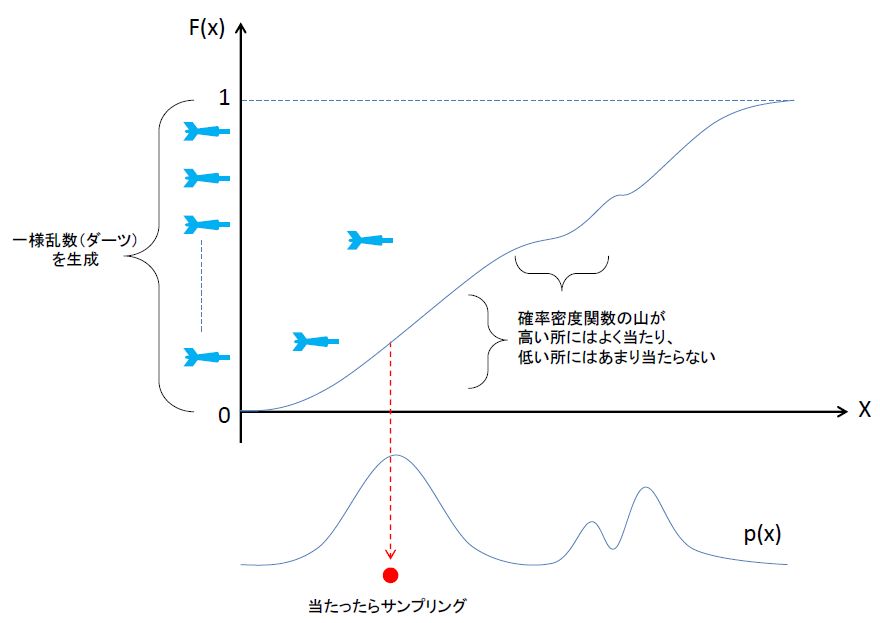
た山が低いところほどなだらかになります。まず、区間[0,1]から一様乱数をひとつ生成します（これを便宜上ダーツと呼びます）。先ほどの累積分布関数に向かってダーツを投げれば、壁が大きいところほど当たりやすく、なだらかなところほど当たりにくいことがわかると思います。ダーツが当たったところの座標をサンプリング点とし、本のダーツを投げれば、確率に比例したサンプル点が得られることがわかると思います。
以上のイメージを元にサンプリングの擬似コード^※1※2を示します。

// サンプル（パーティクル）の定義
typedef struct samples {
double weight; // 確率
int x; // x座標
int y; // y座標
};

// 累積分布関数を計算
double cdf[N];
cdf[0] = samples[0].weight;
for ( int idx = 1; idx < N; idx++ ) {
cdf[idx] = cdf[idx-1] + samples[idx].weight;
}

// サンプルをコピー
copy_samples = copy(samples);
for ( int current = 0; current < N ; current++ ) {
// 一様乱数（ダーツ）を生成
double darts = rand();
// ダーツが当たった箇所を探す
for ( int pre = 0; pre < N; pre ) { if( darts > cdf[pre] ) { // まだ当たってない
continue;
} else { // 当たった
// その場所のサンプルを新たなサンプルとする
samples[current] = copy_samples[pre];
}
}
}

ここまでで、人がいる確率が高い場所にパーティクルをサンプリングするまでの準備が整いました。ただし現時点では、サンプル点が画像上に存在するだけであり、人が何人いるかがわかっていません。サンプリングされた点をクラスタリングすることで、人数の推定をすることが次の課題です。

※1
疑似コードでは述べませんでしたが、各サンプルの確率の値として以下を用いました。

ここでは正規化定数、はそれぞれ、パーティクル（サンプル）がある画素のRGB値を表しています。
今回は白壁が背景であることから、パーティクルのある場所の画素値が白色から遠いほど人である確率が高いだろうと仮定しました。もちろんこの式を変更する事でもっと性能のよい検出を行う事ができます。
※2
新たなサンプルをコピーする際（コードの最終行）、実際には座標に多少のノイズを加えてパーティクルを散らします。あわせて、動体の移動方向がモデル化できるときはその分も考慮して座標を調整することで追跡性能を向上できますが、今回の問題設定は動体のモデル化を行っていないため割愛しています。

• 動体検出　その1
• 動体検出　その2
• 動体検出　その3
• 動体検出　その4